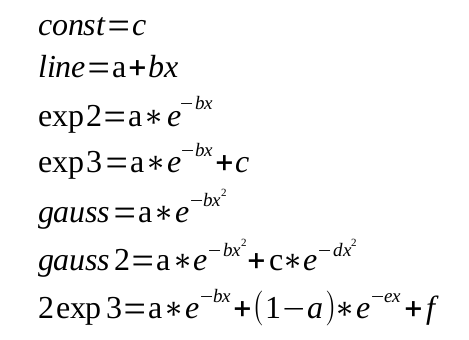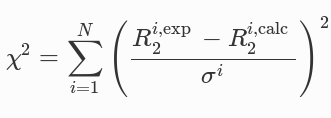GLOVE (Global and Local Optimization of Variable Expressions) is a non-linear least squares fitting program written in C++. It is a flexible
program able to fit most analytical functions. The software runs in the Linux and MacOS environments.
GLOVE_HOME - Original page and Binaries
Manuscript - Article on the software
Source Code - use "unzip glove2.zip" to extract
The details of the program can be found in the manuscript and I'll leave them to the reader. A tutorial taking the reader thru the NMR data processing
to GLOVE fitting routine can also be found at our
Kinetics routine.
Here I'd like to focus on the basics of the
program and what it can do for a chemist. For example, someone interested in fitting a simple 3 parameter exponential to extract kinetic
information from their NMR data. First lets look at some of the features:
- Able to fit most any defined analytical functions.
- Allows fitting with Global parameters. This means if you have several curves all describing the same process (eg several decaying signals
in you NMR spectrum) then you can fit them simultaneously using a single Rate constant for example. The other parameters, pre-exponential and y-offset are allowed to vary however on an individual curve basis. More on this later.
- Perform robust error analysis via Monte Carlo or through Jack Knife simulations
- Can confirm or deny increasingly complex models (eg single exponential vs. multi-exponential) then by analyzing reported Chi squared values and F Statistics.
- GLOVE uses several methods ONE, ONEEX, GRID, RANDOM, MCMIN to set up initial parameters , which are later minimized
with the Levenberg-Marquardt algorithm (LMA)
- Basically these are methods to kick the stuck parameter out of a well which isn't the true minimum.
- Generates plots in XMGR format
- Neatly puts all plots together into a single PDF file as well for quick viewing
Here is a partial list of equations we can fit. eg) to define double exponential we would define the function '2exp3' in the setup.
Each function gets minized wrt chi squared:
where σ is the error bar value.
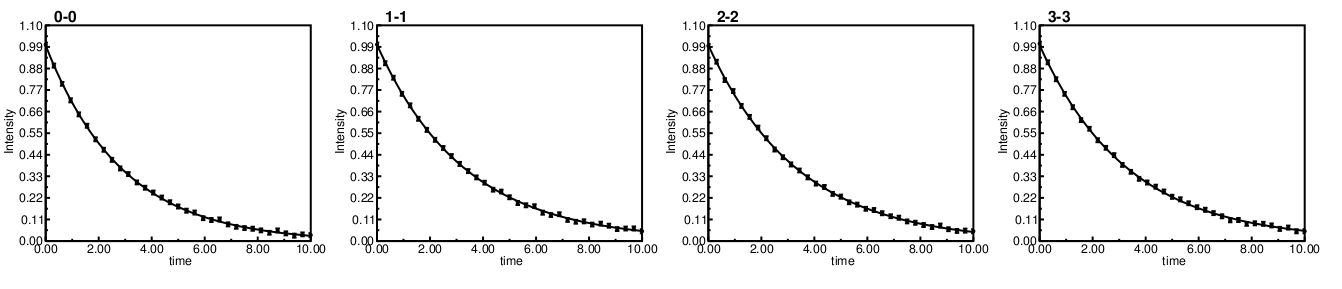
Consider fitting 4 simulated data sets 'individually' with defined values:
rates: 0.35, 0.30, 0.30, 0.30.
Number of pts: 32
Noise level: 1%
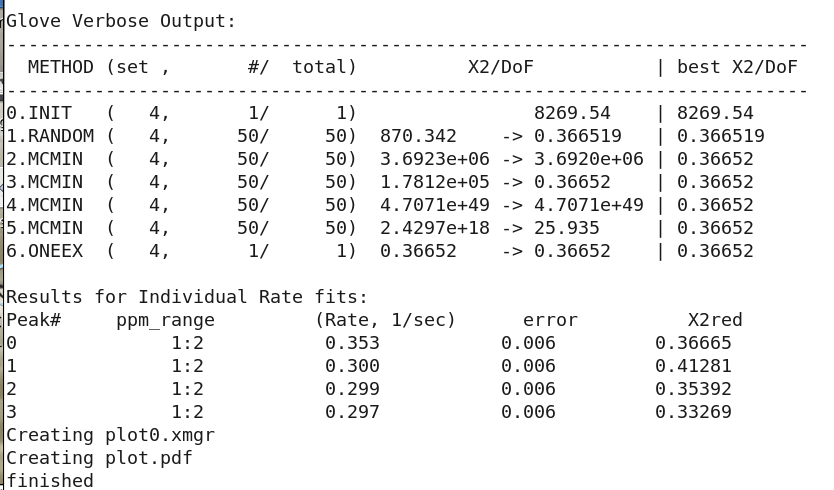
The GLOVE data fitting output results:
While the resulting plots generated and grouped into a single pdf looks like:
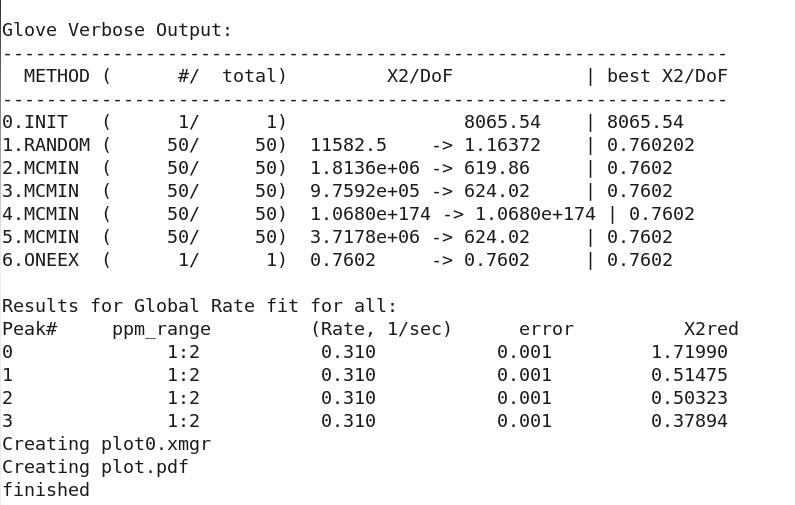
First reported is the 'Random' routine setup χ2 value. Then Monte Carlo is performed several times with tightening criteria. It can be seen
however, that the χ2 value is quickly converged after the first Monte Carlo annealing. Also reported are the χ2 values for each fit. They are
all under 1 and thus are considered quite good.
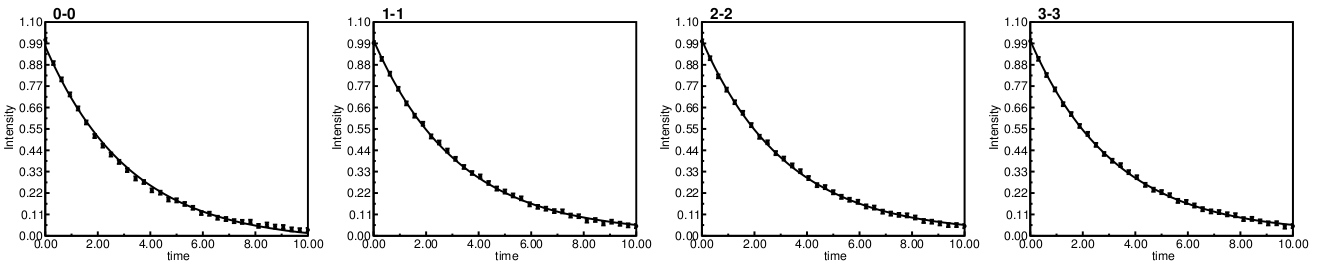
Now lets consider fitting the same data with a single Rate constant aka global parameter for all data sets.
The GLOVE Data fitting output looks like:
While the resulting plots generated and grouped into a single pdf looks like:
Note all the peaks 0-3 all have the same reported Rate=0.31.
Now peak 0 which should have a Rate=0.35 is underestimated at 0.31. It does have significant jump in χ2, as expected, and would easily be identified
as not behaving the same kinetics as the other data sets/peaks. This would be one application of local vs. global fits for identifying groups of peaks
reporting on the same kinetic process. Chi squared ratios of global/local > 2 are a rule of thumb flag for different processes or models. In this case
we have: 1.7199/0.36665 = 4.7 and is clearly out of range.