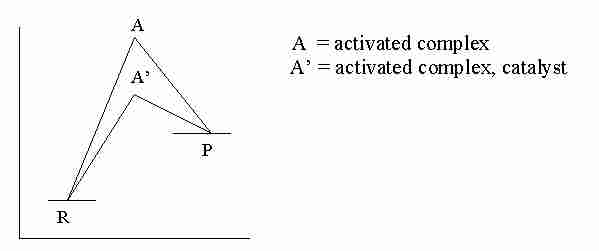
A. Concept.

rate =

Usually expressed in terms of reactant

:

^Rate:

Because it is a reactant a minus sign is used to make rate a positive quantity.
Concentration will be expressed in moles/liter; time may be in seconds, minutes, years. . . .

B. Dependence on concentration of reactant(s)

Generally, m and n are positive integers (1,2,3). However, they can be 0 or a fraction such as ½.
See overhead #3

Determination of m and k from rate-concentration data:

	CH3CHO(g)	CH4(g)	CO(g)
Rate	2.0 M/s	0.50 M/s	0.080 M/s
Conc. CH3CHO	1.0 M	0.50 M	0.2 M

rate 1/ rate 2 = (conc. 1/conc. 2)^m; ** KNOW! Very important!

2.0 / 0.50 = (1.0 / 0.50)^m m = 2 Second Order
hence, rate = k(conc. CH₃CHO)²
k = rate (conc. CH₃CHO)² = (2.0 M/s) / (1.0 M)² = 2.0 M^-1s^-1,

See Overhead #4 See Figure 18.1 p.617

You CAN'T look at the balanced equation and write a rate expression.
It must be done experimentally. (see top of p. 617). Table 18.1

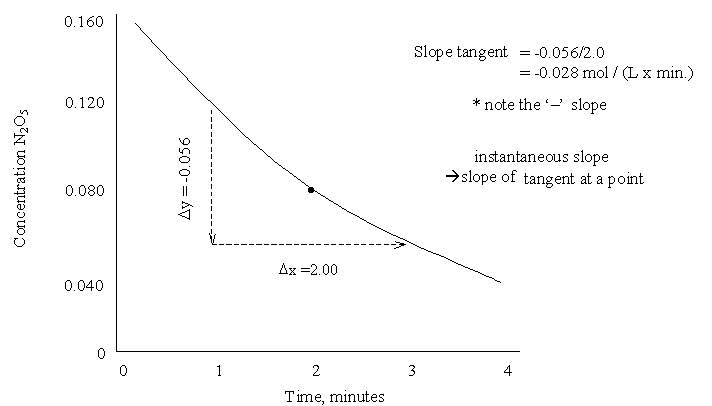
2N₂O₅ 4 NO₂ O₂

Rate = -conc./ time = - [N₂O₅] / t

Rate = k [N₂O₅]¹ 1^st order
           k = Rate Constant

Rate = k (conc. N₂O₅)
k = a rate "constant". . .but it does depend on temp.!
here m = 1 so 1^st order

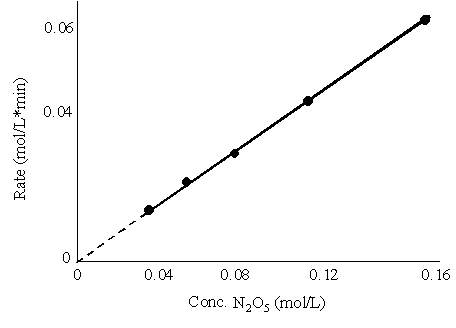
Figure 18.2, p. 619

You need to be able to look at data like this and write a rate expression:

Do Separate             Rate 2/Rate 1 = ([conc. 2]/[conc. 1])^m

Table 18.2 Initial Rates of Reaction (mol/L · s) at 55°C for

(CH3)3CBr(aq) + OH-(aq) ®  (CH3)3COH(aq) + Br-(aq) Series 1  Series 2
	(CH3)3CBr		OH-			(CH3)3CBr		OH-
	(mol/L)		(mol/L)		RATE	(mol/L)		(mol/L)			RATE
Expt. 1	0.50		0.050		0.0050	1.0		0.050			0.010
Expt. 2	1.0		0.050		0.010	1.0		0.10			0.010
Expt. 3	1.5		0.050		0.015	1.0		0.15			0.010
Expt. 4	2.0		0.050		0.20	1.0		0.20			0.010

Rate = k(conc. (CH₃)₃CBr)^m(conc. OH^-)ⁿ

Rate = k(conc. (CH₃)₃CBr)(conc. OH^-)⁰ = k(conc. (CH₃)₃CBr)

C. First Order Reaction

ln X₀/X = kt; X₀ = original conc., X = conc. at time 't'

Suppose k = 0.250s^-1, X₀ = 1.00 M. What is the concentration of reactant after 10.0 s?

 

HALF LIFE

-t_1/2 is independent of original concentration.

It takes as long for conc. to drop from 1.0M to 0.50M as it takes
to drop from 2.0M to 1.0M.

-t_1/2 is inversely related to 'k'. If t_1/2 is small, 'k' is large and vice versa.

So ln X₀/X = kt_1/2 = ln 1/ (1/2) = ln 2. . . see overhead #6

---

ln X₀ - ln X = kt or ln X = -kt + ln X₀, which takes this form y = mx +b
See Overhead #7

---

Rate = -dx/dt for 1st order, rate = kx

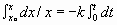
                                                                                      KNOW! ¯                    

ln X – ln X₀ = -kt       OR      ln X₀ – ln X = kt  Þ ln X₀/X = kt

              ln x = -kt + ln X₀          -k = slope, ln X₀ = y-intercept

Figure 18.3, p. 625à  For a first-order reaction, a plot of ln conc. vs time is a straight line.

Zero order: x = x₀ – kt; plot of conc. vs time is linear

     Second order: 1/x – 1/x₀ =kt; plot of 1/x vs. time is linear.

A.    In order for reaction to occur upon collision, reactant molecules must possess a certain minimum energy.  Otherwise the collision is elastic—nothing happens.  See Overhead #11

B.    Catalysis—Catalyst increases reaction rate without being consumed in the reaction  This happens because catalyst furnishes an alternative path for reaction with lower activation energy.

Example: 2H₂O_2(aq) ® H₂O + O_2(g)

Direct reaction comes about by collision between H₂O₂ molecules; E_a is high. 
Reaction is catalyzed by I^- ions:

E_a much lower for two-step process

     In general, increase in T increases the rate.  Rate is approximately doubled when T increases by 10°C. “The story you should be able to tell:”

E

Ea

Also see Overhead #14, and Page 633 of your textbook.

 Relation between k and T: “Arrhenius equation”
ln k = A – E_a/(RT)        R = 8.31 J/K, is in joules

I claim this is in the form of a linear equation 

Y = mx + b                        ln k   = -E_a/[R(1/T)] + A

So a plot of ln k vs. 1/T is a straight line with a slope of –E_a/R

OR –E_a = -8.31 · slope.  See Overhead #15, page 635 in text.

What may be more useful to you is the 2 point form of the equation:

     ln [k₂/ k₁] = [E_a(T₂ – T₁)] / (R T₂ T₁)

Problem: Suppose the rate doubles as T increases from 25°C to 35°C. Find E_a?

Solution: ln [k₂/ k₁] = ln 2 = (10 · E_a) / [(8.31)(298)(308)]

     E_a =5.3 x 10⁴ J or 52 kJ

Suppose k = 0.0251s^-1 at 0°C, E_a = 116kJ.  
Calculate k at 100°C.

  ln k₂/ k₁ = (1.16 x 10⁵)(100) / [(8.31)(273)(373)] =13.7

           k₂/ k₁ = 9.1 x 10⁵

k₂ = (9.1 x 10⁵)(0.0251s^-1) = 2.3 x 10⁴s^-1

     Most reactions take place in a series of steps.  This ordinarily results in a rather complex rate expression.  To find the rate expression for a multi-step mechanism:

1.      Focus on the slow step (rate determining step); assume rate for that step = overall rate.

2.      Coefficients in rate determining step = order of reaction.

3.      Eliminate any unstable intermediates from rate expression.

X₂ + A₂ ® 2AX

1-4. . .elementary steps. 

Most reactions consist of a set of bimolecular steps.

X and A are Intermediatesà a species produced in one step but consumed in a later step.

--The Rate expression is for the slow step.

              Rate = k[X][A₂]

But  X is an intermediate!
So. . .

              K_C = [X]²/[X₂]              à solve for [X]

      [X]²= K_C  [X₂]          or          [X] = (K_C[X₂])^1/2

Replace [X] above

Rate = k · K_C^1/2 [X₂]^1/2 [A₂]        or      Rate = k¢ [X₂]^1/2 [A₂]

--An intermediate is NOT the same as an activated complex.

              Look at overhead #8

IO^- is an intermediate

I^- is a catalyst (Used up then reformed)

Given the following mechanism:

                            k₁

     NO   +  Cl₂   Û   NOCl₂

                             k₂

     2NO   +  Cl₂   Þ 2NOCl

1.    What is the rate expression?

Rate = k₂ [NOCl₂] [NO] 

K_c = [NOCl₂] / ([NO][Cl₂])      

OR         [NOCl₂] = K_c [NO] [Cl₂]

So RATE = k₂K_C [NO]²[Cl₂],                            k₂K_C = k¢