Post. 2 restriction we need real observables

let A | i > = a_i | i >

<i|A|i> = <i|A|i>*

a_i|i> = a_i*|i>

(a_i-a_i*)<i|i> = 0 ==> a_I = a_i*==> a_i real since <i|i> is positive definite

i.e. for

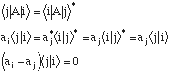, a_j*à a_j since real, <i|j> flip order on complex conj.

either a_i = a_j (same state or degenerate) or orthogonal: <i|j> = 0

if |i>, |j> are degenerate can construct ,

<1|2> = 0, orthogonal by construction and still are degenerate eigen functions

i.e.

Applications:

The wave function describing the state of a quantum mechanical system can be described as a superposition of in terms of eigen functions of an operator --{f_i},

since they form a complete set

You have experience with this from

Taylor series: or

so f(x) is represented as linear combination of xn -- power series

More general is Fourier series :

where expand in sine and cosine fcts or exponetials:

(Note sin is odd, must add cos if parity not odd, eliminate sin if even)

So what are the coefficients? In Taylor : but

multiply. by g_j* and integrate :

Dirac delta function: <i|j> =

part of |f> that lies along |i> [analogous to dot (scalar) product from vector algebra]

is only non-zero for f = gi or f-degenerate with g_i , (otherwise , orthog)

alternatively: if g_i are indep fct, only if will ci be non-zero: ,

A commutator of operators , is

Note this is familiar: from Post 2

Simple multiplicative or scalar operators commute -- this is your experience

derivative and matrix operators may or may not commute.

if we say it commutes

???errorsimple proof not general: let {fi} be eigen fct ,

book proof a little more general -- uses commutation of constants, ai, bi

This theorem very powerful, lets us substitute eigen functions to determine properties.

Also this is uncertainty principle : if

then we can determine observables corresponding to , with arbitrary accuracy

if not uncertainty relation tells measurement limitations

recall: operator must act on something: (d/dx)xf(x) = f(x) + x(df(x)/dx) è Chain rule differentiation leaves a noncancelling term

Reverse form particularly important

let set of eigen functions

Commutation has form of uncertainty (recall <==> )

use expectation values and mean deviation:

since is a constant:

let iC represent result of commutator can be zero, a constant or operator

then from:

define root mean square deviation:

but a consequence of time dependent Schroedinger Equation

even: f(x) = f(-x) , f(x,y,z) = f(-x, -y, -z)

odd: f(x) = -f(-x)

if system has parity it is even or odd and that can be represented by parity operator

gi = cigi gi - odd - ci = -1 gi eigen fct of

= gi(-x, -y, -z) ci - even - ci = 1 all possible even/odd fct

if these eigen fct of must be even/odd

but depends on form of potential

e.g. (Hooks law spring) even -- square of coordinate

(electrostatic attraction) even --depends only on distance, not direction

(change in electric field is directional - odd)

V = even

ex. 1 let V = +1 ,

V = -1 1 > x > -1

this is even, has definite parity, is eigen fct of parity operator

These concepts are central to applications of group theory and symmetry to molecular q.m. problems and spectroscopy.

Test:

= 0 if V even ‚ 0 if V odd or mixed parity

recall make a measurement on some normalized state 4

p_i is |c_i|² or probability of measuring each ai

and

[If ai degenerate, probability is sum of for degenerate ai]