POSTULATES OF QM -- Levine Ch 7

POSTULATES OF QM -- Levine Ch 7.8, Atkins Ch. 5, R&S - Ch 2.

Much as in thermodynamics, one can establish a set of "laws" which we have called "postulates" (since they have non-obvious physical relationship) and then derive all QM properties from these

point -- value lies in how well they describe nature

if work à keep them, if fail à devise new theory

Postulate 1.

The state of a system is fully described by the wave function, (r1, r2, ... t)

--where r1, r2, ... are positional coordinates of each particle 1,2 ... and t is time.

"fully described" all that we can know -- is anything we can measure.

Quality of (r1, ... t) as a function (Sch. rep.)

single valued --drawing1

continuous --drawing2

integrable square --

Since (r1, ... t) contains all info--could list quantum numbers-"code" values

| a,b,c ...> = state Dirac bra-ket notation < a,b. .| . . | a,b . .>

# of independent q.n. will reflect the dimensionality of problem

e.g. 3-D vector fct require 3 indep. fct 3 quantum num.

Interpretation: probability in area

system is in the state

Postulate 2.

To every physical observable there corresponds a linear, Hermitian operator.

For any classical observable convert to q.m. operator by: these "operate" on wave function:

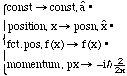
ex: energy: T = p²/2m , V = V(x), E = (const., conserved system)

linear:

This is necessary to probe the probe the properties of systems that one in mixed states on in state representation by superposition of other wave functions

Hermitian (Levine 7.2) -- has to do with observables being real

quantum measurement has parallel to probability

probability any value probability of measured quant

evaluation generally:

to guarantee real need: <a> = <i|a|i> = <a>*

Hermitian more generally:

in Dirac symbolism . Hermitian

can even compress further as a_ij = < i |a| j> represent a matrix

these evaluate "probability" of system being in a state defined by f_i and af_j

Eigen value equations (Levine 7.3) This is Levine Postulate 4

for every operator there will be a set of functions that fulfill eigen value equation

af_j =af_I where {f_i} are set of eigen functions

Dirac notation: a|i> =a_i|i> ai -- eigen value is a constant

This set of functions will completely describe the space upon which the operator can operate, so any wave function representing state of system can be expanded as linear combination of set: -- or superposition of eigen functions.

{f_i} set of eigen functions

since set of f_i, is complete, in Dirac set of |i> is basis for a general vector

Now effect of operator has changed

This is not an eigen value equation relationship since

const

[the mixing of fi components to make up is now changed]

or where g is a new function/state

Degenerate eigen fcts: and

then f and g said to be degenerate (save eigen value)

but also any linear combination of f and g degenerate:

ex. - p orbitals any comb. still a p orbital in absence of magnetic field

ex: Schroedinger eqn. , - total energy op., E - const. of motion

classical H = T + V =

1-D, single point or 3-D

Monday -- August 27

So how do we make measurements?

Postulate 3. (Postulate 3¢ - Atkins) (deviates a bit from Levine)

Where a system is in a state characterized by and is an eigen function of which is the operator representation of some observable, with an eigen value of a, then measurement of that observable on a system will uniquely yield the eigen value a, every time.

if the system is in a state , then every measurement of a yields a

ex. -- easiest example is energy. If a particle has a well-defined (conserved) energy for state : each measurement yields or

Clearly if molecule in a superposition of states: where

Then measurement of energy would not be well defined -- no eigen value:

‚( const) y

Postulate 4. (Post 3-Atkins, Post 5-Levine)

The result of measurement of any property, whose operator representation is , on a system in a state, , the average value measure is given by the expectation value