Chapter 7

THERMODYNAMICS

 

Fundamental Definitions

System: That part of the universe within some definable boundaries

Surroundings: Everything in the universe outside of the system

 

Types of Systems

Open System: A system that can exchange both matter and energy with the surroundings

Closed System: A system that can exchange energy, but not matter with the surroundings

Isolated System: A system that cannot exchange either matter or energy with the surroundings

 

 

 

Practice Problem on Classifying Different

Types of Systems

 

Classify each of these systems as open, closed, or isolated

A  thin-walled glass sphere 

CLOSED       

 

 

 

A beaker containing a solution

OPEN

       A well-insulated, sealed box

                                            ISOLATED

 

 

Note that an isolated system would have no way of knowing that the rest of the universe even existed!

Some very fundamental concepts regarding the essential nature of thermodynamics.
  1. Pure thermodynamics deals only with the macroscopic properties of matter. It makes no assumptions whatsoever about the existence or nature of the particles of which matter may be composed.
  2. Thermodynamics is concerned with the equilibrium states of systems.
    1. It does not concern itself with the rate at which a process occurs—this is dealt with under the topic of chemical kinetics.
    2. It does not attempt to describe a system while a change is taking place.
    3. It does not tell us if a given change will take place, but only tells us if a given change can occur in principle, which essentially means that such a change would not violate one of the laws of thermodynamics.

 

 

 

STATE FUNCTIONS

The thermodynamic description of a system is accomplished by specifying the values of certain quantities called state functions.

State functions have two important properties.

    1. By specifying the values of a few of the (2 or 3), the values of all the others may be calculated.
    2. Changes in state functions depend only upon the initial and final states of the system, and do not depend in any way upon how (the path) the system is transformed from the initial to the final state.

Common State Functions and Their Accepted Symbols

Volume V

Temperature T (always in K)

Pressure P

Energy E

Enthalpy H

Entropy S

Free Energy G

Example: State Functions and Some Changes

For one mole of an ideal gas

Initial State

P1 = 1.0 atm V1 = 22.4 L T1 = 273 K

Final State

P2 = 10.0 atm V2 = 4.48 L T2 = 546 K

Changes

DP = P2 - P1 = 10.0 – 1.0 = 9.0 atm

DV = V2 - V1 = 4.48 – 22.4 = -17.9L

DT = T2 - T1 = 546 – 273 = 273 K

Important Convention

A change in a thermodynamic quantity is always defined as the final state minus the initial state. Adherence to correct sign conventions is critical when working thermodynamics problems.

Example:

DT = TF – TI

 

 

 

 

HEAT CAPACITY

 

(Know page 211)

Heat Capacity: The amount of energy required to change the temperature of a material by one Celcius (or Kelvin) degree. (Units J/o C)

Note: A related quantity which really measures the same thing, is something called the specific heat of a substance, which is the amount of energy required to change the temperature of one gram of a material by one Celcius (or Kelvin) degree. (Units J/g o C)

Practice Problem

The specific heat of solid iron is .4570 J/g o C. If 35.0 g of pure iron, initially at a temperature of 150.0 o C, is added to 125.0 mL of pure water, initially at a temperature of 25.0 o C, what will be the final temperature reached by the system?

Assume a specific heat for water of 4.184 J/g o C and a density of 1.00g/mL, and that no heat is lost to the surroundings.

Let the final temperature reached = TF

(When thermal equilibrium is reached)

Heat lost by Fe = Heat gained by H2O

Heat à DE = M x DT x S.H.

 

TiFe = 150.0 o C                 TiH2O = 25.0 o C

MFe = 35.0g                       MH2O = 125.0g

S.H.Fe = .4570 J/g o C      S.H.H2O = 4.184 J/g o C

-qFe = qH2O

-[ MFe x (TF – Ti ) x S.H.Fe ] = MH2O x (TF – Ti ) x S.H.H2O

Ok pal work it out now!

 

The answer is 28.7o C

 

 

DE = M x DT x S.H. = q

DT = (TF –Ti )

S.H. H2O = 4.184J/g 0 C = 1.00 cal/g 0 C

See table 7.1à Water has a high S.H. (p. 213)

Exothermicà q<0       Endothermicà q>0

See p. 215

qReaction = -qcal

See OH#9

qReaction = -[Ccal ] x DT

    Ccal  is really    Heat Capacity J/0 C (p. 216)

Enthalpy (H) = Heat Content

qReaction = DH = HP – HR

therefore, exothermicà DH<0; endothermicà DH>0

C2H5OH + 7/2O2 à 2CO2 + 3H2O

 

 

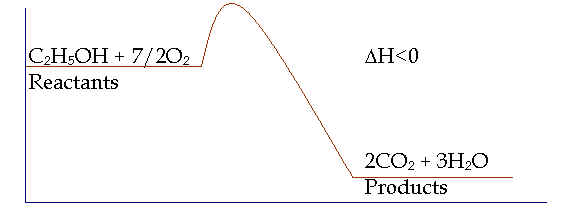
Reaction Path

See p. 218à Note law of conservation of energy

C2H5OH(l) + 7/2O2(g) à 2CO2(g) + 3H2O(g) + 1238.7 kJ/mol

 

DH = -1238.7 kJ/mol Very important

Laws of Thermodynamics

  1. See p. 220 for #1 DH and stuff (See above equation)
  2. See p. 221 for #2

    2CO2(g) + 3H2O(g) + 1238.7 kJ/molà C2H5OH(l) + 7/2O2(g)

    DH = 1238.7 kJ/mol

  3. See p. 222 for #3 Hess’s Law

The Second Law of Thermodynamics LINK!

Back to the Class Notes Homepage
 



Maintained by: Chris Weilemann

Lee Marek