...this is Mr. Marek's AP Chemistry notes...

AP Chemistry - Chapter 5 Notes
The chemical properties of atoms are determined by the way in which the e- are arranged about the nucleus. If we know the electronic structure of an atom, we can predict much of the chemical behavior of the element(s). That is the point of this chapter.

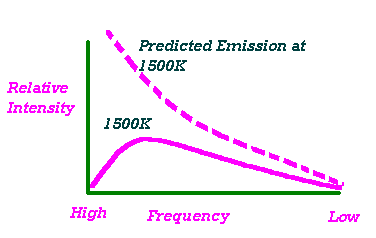
Blackbody Radiation

Prior to 1900, light was assumed to simply be an electromagnetic wave. As such, the energy carried by a light wave was proportional to the sum of the squares of the amplitudes of the electric and magnetic waves.

E a (E2 mass + H2 max) a Light intensity

Notice that the frequency of a light wave has absolutely nothing to do with the energy carried by the light.

The chemical properties of atoms are determined by the way in which the e- are arranged about the nucleus.

 

Results of Blackbody Radiation Experiments

 

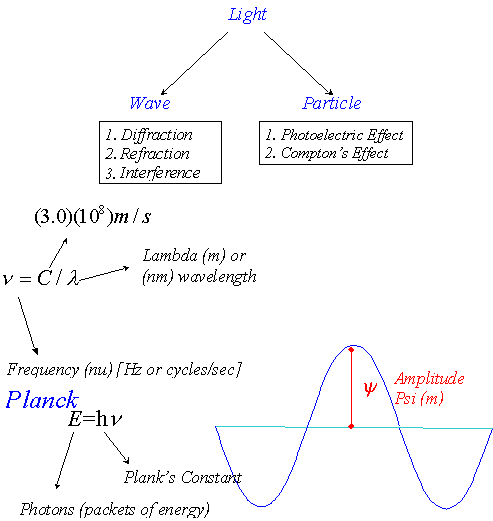
Planck’s Explanation
  1. Light of frequency n is emitted by an atom or a group of atoms that are oscillating with a frequency = n .  n =c/l
  2. The energy of an oscillator is restricted to only certain allowed values. These allowed values are dependent upon the frequency of the oscillator, and are given by the equation

    3.

    where n is a positive integer, and h is Planck’s constant.

  3. If an oscillator is to emit energy, it must change from a higher energy state to a lower energy state. Consequently,

    4.
  4. Planck assumed that the oscillators were in equilibrium with each other and that their energies were distributed according to Boltzmann’s distribution. This meant that the chance of finding an oscillator of e =nhn was proportional to e-nhn /kT. Since e-nhn /kT decreases exponentially as nhn increases, the chance of finding high frequency oscillators is very small. Consequently, the amount of high frequency light given off should be very small. This resolves the ultraviolet catastrophe.

            Know: n =c/l & E=hn

 

Balmer’s Formula – 1885

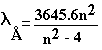where n = 3,4,…

or

Gave the correct visible lines.

 

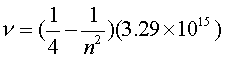
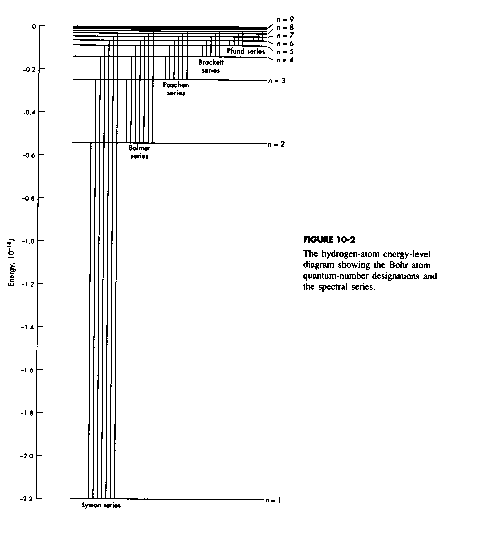
Spectrum of the H-Atom

There are several groups of lines all following the general qualitative pattern.

           

Ultraviolet – Lyman Series

Visible – Balmer Series

Infrared – Paschen Series

Lyman Series Energies

984.1 kJ/mol
1166.3
1230.1
1259.6

1312.1

Balmer Series

182.2 kJ/mol
246.0
275.5
291.6

328.0

It took something / someone to go from here, someone to make a paradigm shift, to show that matter can act as a wave and as a particle.

Bohr was the "intermediate" between the "old" physics (Newton physics) and the "new" quantum physics."

Predestination vs. Determinism

The main contribution of Bohr, as we shall see, was to devise a model for the atom and demonstrate, by the aid of a model, that he could account for spectral lines in terms of energy levels within the atom.

However, there was one slight limitation…

it only worked for 1 e- (electron) systems!

BOHR POSTULATED: Radius of an orbit is fixed by the requirement that the force of attraction between a nucleus or charge Ze, an electron of charge e- is given by COULOMB’S LAW

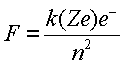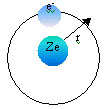Also, the centripetal force of the electron moving in an orbit may be written as…

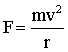m = mass of e- 
v = velocity
r = radius

 

We have two forces again:

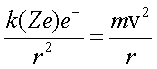
Now Bohr imposed a Quantum Condition because it worked (hard to accept that)!

Angular Momentum  mvr = constant

n = 1, 2, 3, … positive whole numbers
h = Planck’s Constant

Bohr found:

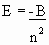
See p. 138

De Broglie. His idea brought matter and waves together. He said, matter, like light or any E.M.R. can act as both a wave and a particle.

Louis de Broglie’s Derivations

Plank             Einstein
E= hn             E=mc2

SO setting them =             hn =mc2

replacing n =c/l

we get hc/l =mc2

or

l=h/mc

Matter does not move at the sound of light…

soooo l = h/mc becomes l = h/mv

l = h/mv where V is speed

Matter waves!
For an electron orbiting in a circle:
2p r = nl

2p r = nh/mvl

mvr = nh/2p
 What Bohr had assumed!

What does this mean?! 

See p.142

One needs a fixed number of waves or else one will get interference of waves. The waves have to fit on a circle so you need a whole number of waves.

nλ = 2πr

"Proved" by Davisson and Germer in 1927 at Bell Labs when they found diffraction patterns for e- just like light:

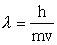    (note: the larger the object, the smaller the l )

 

Heisenberg Uncertainty Principle

The inability to predict both the exact location of atomic particles and their momenta at the same time:

(D P)(D x) » h

D P = momentum = mv D x = distance

So, we end up speaking about where the e- is and its momentum in terms of probability

 

A new model had to be developed:

Quantum Mechanics

We need to use Probability!

See p. 132, 133 Use (d - Salt)

D E = hn =h(c/l )                 l =h/(mv)

Know these 3 equations!

Wave model developed by Schröedinger flooded planet model.

Wave characteristics to electrons (p. 144)

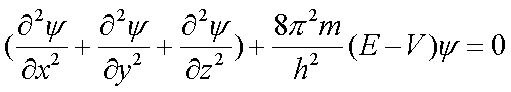
x, y, z ą space coordinates

m    ą mass of an electron (e-)

E    ą total energy of electron-proton system

V    ą potential energy

y      ą (Greek letter, psi) amplitude of wave function

Solutions yield expressions for y and certain quantum numbers pop out. These values determine the allowed energy states of the electrons and the shapes of the space the electrons occupy.

y2 is the probability of finding the electron in an element of unit volume about the nucleus.

y 2 µ the electron cloud density

 

Electron clouds are probability regions in space where the electron (e-) is likely to be found. We call these orbitals. Each orbital has associated with it a set of quantum numbers (like an address):

(n, ℓ, mℓ)

 

These come out of the Schröedinger equation (see p. 145)

 

 

Wave model developed by Schröedinger flooded planet model.

Wave characteristics to electrons (p. 144)

     n The Principal Quantum Number

The value of n determines to a large extent the ENERGY of an e- and is related to the average DISTANCE of an e- from the nucleus. (Also periods in table)

n=1 is the lowest

n comes in positive whole numbers

In a given energy level there are 2n2 e-

 

As n , E , and as n , Volume

n also indicates the number of nodal surfaces associated with each orbital.                               

Location where probability of finding an e- is zero.

 

ℓ Is directly related to the SUBLEVEL and hence the SHAPE of the orbitals

l is determined by n. It may take on values of 0 to n – 1.

n = 1             ℓ = 0

n = 2             ℓ = 0 or 1

n = 3             ℓ = 0, 1, or 2

n = 4             ℓ = 0, 1, 2, or 3

Value of ℓ Sublevel Type Maximum # of e-
0 s 2
1 p 16
2 d 10
3 f 14

mℓ Gives us the directional characteristics of the sublevels (Š    )

mℓ takes on the values of + ℓ, …, 0, …, – ℓ.

 

l

 

ml

 

Sublevel

0

0

s

1

+1, 0, -1

pxpypz

2

+2, +1, 0,-1, -2

d’s

In a given sublevel there are 2 l +1 orbitals. ml tells us what orbital we are in.

Cool site for f orbitals see http://www.albany.net/~cprimus/orb

ms SPIN: an e- behaves as if it were spinning. A spinning e- gives rise to a magnetic field, up or down. This is like 2 magnets in opposite directions. This is why you can get 2e- in the same orbital. (see p. 148)

ms takes on values of +1/2 or –1/2

PAULI EXCLUSION PRINCIPLE

(Know it!!!) See p. 149 all red

See OH 28

See p. 152 Fig. 5.11

 

                                                                     Electron Configuration
AUFBAU (Building Up) Electron Box Diagram

See. P. 153

See OH 29, 30, 31, 32

HUND’S RULE See p. 155, 156

Monatomic Ions - Representative Elements

    • Transition elements
    • See p. 159

   

Back to the Class Notes Homepage
 



Maintained by: Chris Weilemann

Lee Marek