Lee Marek's Website - Advanced Placement - Class Notes

CHAPTER 20

The basic goal of chemistry is to predict whether or not a reaction will occur when reactants are brought together.

One way is if ΔH<0 reactions tend to go SPONTANEOUS

If K>1 reactions tend to go

If ΔE is + [next chapter] reactions tend to go

If ΔG is –

"Nature tends to move spontaneously from a state of lower probability to one of higher probability."

G.N. Lewis – IN YOUR TEXT – p. 693

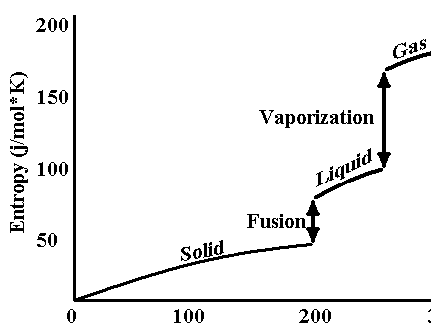
Entropy: describes the randomness involved in energy transactions. A system that is more random has a higher “S”. So ΔS is + means products are more random than reactants.

It is a State function – See fig 20.5 and p 697, nice job in text.

Spontaneous Reactions

Examples: H₂O_(s) à H₂O_(l) at 25 C
CH_4(g) + 2O_2(g) à CO_2(g) + 2H₂O_(l)

Factors Affecting:

Energy factor: at 25 C, 1 ATM, exothermic reactions are ordinarily spontaneous (HO)

Randomness Factor: Other things being equal, systems tend to move from a more ordered to a more random structure.

temp(K)

II. Entropy Changes

See table 20.1 note units. Note elements have S^o unlike Δ H. Why? See p.700;table 20.2

Once again, H⁺ Zero – Zippo – "0" – none

Note: S is + for elements and compounds.

ΔS = ΔS _products –ΔS _reactants

Measure of Change in ordering

Solid à liquid; ΔS +

Liquid à Gas; ΔS +

ΔS is usually + for a reaction in which the # of moles or gas increases. See p. 701

2SO₃(g) à 2SO₂ (g) + O₂(g); Δn_g = ? so ΔS=?

N₂(g) + 3H₂(g) à 2NH₃ (g); Δn_g = ? so ΔS =?

Calculations of ΔS^o (^o means 1 atm, 1M, 25^o C)

ΔS^o = S S^o_products- S S^o_reactants

Fe₂O_3(s) + 3H_2(g) à 2Fe_(s) + 3H₂O_(g)

ΔS^o = 2S^oFe_(s) + 3S^oH₂O_(g) – S^oFe₂O_3(s) – 3S^oH_2(g)

= 2(27.3 J/K) + 3(188.7 J/K) – 87.4J/K – 3(130.6)

_{= 141.5 J/K}

ΔS^o is nearly temp. independent (see p. 702)

Reactions for which ΔS is + tend to be spontaneous, at least at high temp.

H₂O_(s) à H₂O_(l) ΔS= +/- ΔH= +/-

H₂O_(l) à H₂O_(g) ΔS= +/- ΔH= +/-

At what conditions do these reactions become spontaneous?

III. Second law of thermodynamics:
In a spontaneous process, the entropy of the universe increases.

ΔS_univ > 0

ΔS_total = ΔS_system + ΔS_surr > 0

For spontaneous Process

Calculation of ΔS_surr at constant T, P :

ΔS_surr = q_surr/T

ΔS_surr = -ΔH/T (constant T, P)

Show by calculation that the vaporization of water at 25° C and 1 ATM is non- spontaneous
H₂O_(l)àH₂O_(g).

ΔS_system = S^oH₂O_(g) – S^oH₂O_(l) = 0.1188kJ/K

ΔS_surr = -[ΔH_fH₂O_(g) - ΔH_f H₂O_(l)] / T = -44.0/298

ΔS_total = 0.119-0.148 = -0.029 kJ/K

Where would ΔS_total = 0?

IV. Free Energy Changes

∆G° = ∆H° - T∆S° Gibbs/Helmholtz Equation

Note that ∆G, like ∆S, is dependent on P. Unlike ∆H° and ∆S°, ∆G° is strongly temperature dependent because of T in the equation.

If ∆G° is -, reaction spontaneous at standard conditions

If ∆G° is +, reaction non-spontaneous at standard conditions

If ∆G° is 0, reaction at equilibrium at standard conditions

Free Energy: "Real" energy change not only from breaking and forming bonds (Enthalpy), but taking organization changes (Entropy) in account as well.

The striving to achieve a state of minimum free energy may be interpreted as the driving force for a chemical reaction.

Read the last paragraph p.707 & all 708
p. 709 Gives standard conditions
See p. 711 Underline
See OH #6

Comments Regarding "Standard Free Energy Changes"

The free energy of a substance (as well as its enthalpy and entropy) depends upon the state of the substance, i.e., whether it is a solid, liquid, or gas.

In addition, the free energy depends upon the temperature, the pressure, and in the case of solutions, on the concentration.

Consequently, the change in free energy that occurs during a chemical reaction depends upon the state (s, l, g), the conditions (T,P), and the concentrations of the reactants and products.

For convenience, standard conditions have been chosen for reference. These conditions are:

T= 25°C

P= 1 atm

Concentration = 1 M

Standard Free Energies of Formation, ∆G_f°

Definition:

The free energy change when one mole of a substance in its free state is formed from its elements in their free states.

This definition is obviously analogous to our earlier definition on enthalpy of formation, and the calculation of the free energy change which occurs during a reaction is accomplished in a similar manner.

Note: The superscript o, above is a thermodynamic symbol that generally indicates free or standard state.

A QUALITATIVE LOOK at what is Implied by the Equation:
ΔG = ΔΗ - TΔS

Since there are two possible signs for both ΔH and ΔS (positive or negative), there are four possible combinations of these signs.

If both ΔH is negative (good) and ΔS is positive (good), then ΔG must be negative, and a process for which this is true will be spontaneous at all temperatures.

If ΔH is positive (bad) and ΔS is negative (bad), then ΔG must be positive, and a process for which this is true will not be spontaneous at any temperature.

If both are + or -, then ΔG can be either negative or positive depending upon which has which sign and whether ΔH is greater or less than TΔS.

These ideas are summarized in the following chart.

Gibbs-Helmholtz equation: ΔG° = ΔH° - TΔS°

If ΔH° is +, ΔS° is -, then ΔG° is + at all T, nonspontaneous at 1 atm. *

ΔH° is -, ΔS° is +, then ΔG° is - at all T, spontaneous at 1 atm. **

ΔH° is +, ΔS° is +, then ΔG° is + at low T, becomes negative at high T

ΔH° is -, ΔS° is -, then ΔG° is – at low T, becomes positive at high T.

(*)Reverse reaction is spontaneous

(**) Reverse reaction is nonspontaneous

Practice Problem

Consider:

H₂O_(l) à H₂O_(g) at P = 1atm

If ΔH = +40.63kJ, and ΔS = +108.8 J/K·mol. What is the boiling point of H₂O_(l)?

ΔG = ΔH-TΔS At equilibrium, ΔG = 0, so

0 = ΔH - TΔS

ΔH = TΔS

T = ΔH/ΔS = 40630/108.8 = 373 K

* See p.715 – Equation 20.22 KNOW IT!

Practice Problem

Consider the reaction:

3/2 O_{2(g) à}O_3(g)

Calculate ΔG° for this reaction, given:

T = 25°C ΔH_f°[O_3(g)] = 142.2 kJ/mol

S°[O_2(g)] = 205.0 J/K· mol S°[O_3(g)] = 237.7 J/K· mol

ΔG_f° = ΔH° - TΔS°

ΔS° = 237.7 – 3/2(205.0) = -69.8 J/K

ΔG° = +142,200 – (298)(-69.8) = +163,000 J = +163 kJ

Practice Problem

Calculate the free energy change that occurs during the combustion of 6.48 grams of propane, C₃H₈, to form carbon dioxide and liquid water given: @25° C, 1atm

ΔG_f°[C₃H_8(g)] = -23.47 kJ/mol

ΔG_f°[CO_2(g)] = -394.38 kJ/mol

ΔG_f°[H₂O_(l)] = -237.19 kJ/mol

Balanced equation is:

C₃H_8(g) + 5O_2(g) à 3CO_2(g) + 4H₂O_(l)

ΔG° = Σ ΔG_f°(Products) - Σ ΔG_f°(Reactants)

ΔG° = [3 ΔG_f°(CO₂) + 4 ΔG_f°(H₂O)] –[ΔG_f°(C₃O₈) + 5ΔG_f°(O₂)]

ΔG° = [3 (-394.38) + 4 (-237.19)] –[(-23.47) + 0]

ΔG° = -2108.43 kJ/mol C₃H₈

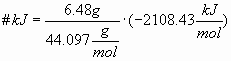
Note: normally you wouldn’t use ΔG°’s: they are very temperature dependent. Instead, use ΔH°’s and ΔS°’s.

ΔG= ΔH -TΔS

***************************************************

Calculate ΔG° at 25°C and at 500°C. Don’t use appendix (for ΔG°’s).

D S° = 2S° _Fe +3S° _H20(g)- (S° _Fe2O3 + 3S° _H2)

Spontaneous at 500ºC, not at 25ºC.

At what temperature does the reduction of Fe₂O₃ by H₂ become spontaneous at 1 atm?

Relationship Between ΔG° and K

Since both the free energy change for a process and the equilibrium constant for a process describe the tendency for the process to occur, it would seem that these two quantities should be related to each other.

Read pg. 720, #1, 2, 3

If K > 1, DG° < 0	Reaction spontaneous at stand. cond.
K < 1, DG° > 0	Reaction nonspontaneous at stand cond.
K = 1, DG° = 0	Reaction at equilibrium at stand cond.

See table 20.4 p. 720

*************************************************

Calculation of DG° for the following reaction:

H₂O_(l) ↔ H⁺_(aq) + OH^-_(aq)
DG° = -(0.00831)(298) ln (1.0 x 10^-14) = +79.8 kJ
Nonspontaneous at standard conditions (1 M H⁺, 1 M OH^-)

Read 721-722
What is the second law of thermodynamics?
You can’t break even!
The entropy of the universe increases!
What is the first law of thermodynamics?

Practice Problem

If the free energy of formation of HI at 490°C is –12.1 kJ/mol, calculate K for H_2(g) + I_2(g) à 2HI_(g)

DG = -RTln K

ln K = - DG/RT

ln K = -(2)(-12.1 x 10³)/(8.314)(763)

ln K = +3.8149

K = e^3.8149 = 45.4

Practice Problem

Consider: 2NO_(g) + O_2(g) à 2NO_2(g)

Given: K = 1.6 x 10¹² and DG_f°(NO) = +86.6 kJ/Mole at 25°C

Calculate DG_f°[NO_2(g)]

DG° = -RTln K

DG° = -(8.314)(298)ln (1.6 x 10¹²)

DG° = -6.96 x 10⁴ J = -69.6 kJ

DG° = 2 DG_f°(NO₂) – 2 DG_f°(NO) =

DG_f°(NO₂) = [ DG° + 2 DG_f°(NO)]/2

DG_f°(NO₂) = [(-69.6) + 2(86.6)]/2

DG_f°(NO₂) = +51.7 kJ

Absolute Entropies

And

The 3^rd law of Thermodnamics

The 3^rd Law simply states that:

The entropy of perfect crystals of all pure elements and compounds is zero at the absolute zero of temperature.

One significant result of this law is that it allows scientists to calculate (and publish for our use) tables of absolute entropies of substances.

The calculation of absolute entropies gets rather involved. Essentially, the calculations use the relationship

DS = nC_pln T₂/T₁ Heat Capacity

but are actually much more complicated, because C_p itself is a function of temperature, and often a very complicated one.

Fortunately, the calculations are done for us, and we simply use the published table of absolute entropies of substances.

Back to the Class Notes Homepage

Maintained by: Chris Weilemann

Lee Marek