Lee Marek's Website - Advanced Placement - Class Notes

Chapter 14

Operational Definition of an Acid

Acids are substances that have the following properties:

Tastes sour.
React with active metals, such as Zn or Al, to liberate hydrogen gas.
Turn litmus red.
Turn phenolphthalein clear.
Conduct electricity.
Neutralize bases.

Operational Definition of a Base

Bases are substances that have the following properties:

Tastes bitter.
Reacts with amphoteric metals, such as Zn or Al, to liberate hydrogen gas.
Turns litmus blue.
Turns phenophthalein red.
Conducts electricity.
Neutralizes acids.

See p.469 Reactions #1&2

Svante Arrhenius-1884
Proposed first "correct" theory of acids and bases that is still being used.

Arrhenius Definition of Acids and Bases

Acid – A substance that produces H⁺ in aqueous solution (or that increases the H⁺ concentration in an aqueous solution).

Base – A substance that produces OH^- in aqueous solution (or that increases the OH^-concentration in an aqueous solution).

Types of Substance that are Arrhenius Acids

"Classical" Acids:

HCl, HNO₃, H₂SO₄, HClO₄, HBr, HI, HC₂H₃O₂, HF, HSO₄^-, H₃PO₄, H₃PO₃, H₂CO₃, etc.

Nonmetallic oxides:

CO₂, SO₂, SO₃, Cl₂O₇, NO₂, P₂O₃, P₂O₅, etc.

Acid Anhydride: a nonmetal oxide that reacts with water to form an acid (acid rain).

H₂O + SO₃ ® H₂SO₄Strong acid

H₂O + CO₂ « H₂CO₃Weak acid

Certain metallic ions, notably those that have a relative high charge and/or, a small radius:

Al³⁺, Cr³⁺, Fe³⁺, and some +2 ions (to a lesser extent).

ALSO NH₄⁺

Types of Substance that are Arrhenius Bases

"Classical" Bases:

NaOH, KOH, Ca(OH)₂, NH₄OH

Ammonia and other organic amines:

NH₃, CH₃NH₂ (methyl amine), C₆H₅NH₂ (aniline), C₅H₅N (pyridine), N₂H₄ (hydrazine), etc.

Metallic Oxides:

BaO, MgO, Na₂O, K₂O, etc.

Basic Anhydride! A metal oxide that reacts with water to form a base.

BaO + H₂O ® Ba(OH)₂

Na₂O + H₂O ® 2NaOH

Substances Containing Anions from Weak Acids:

Na₂S, KC₂H₃O₂, NaHCO₃, NaF, NaCN, etc.

Strong vs. Weaks Acids

Common misuses of the term "strong":
Used to mean highly corrosive
As a synonym for concentrated

Common Strong Acids and their approximate K_aValues:
In order of decreasing strength

HI----------10¹¹HBr--------10⁹HClO₄-----10⁷         Know these (not #’s,
HCl--------10⁷         but which are strong)
H₂SO₄-----10²         See P. 475
HNO₃------20

Note: For practical purposes, all these acids are equally strong in water, i.e., 100% ionized. To distinguish their relative strengths, we must use a "differentiating" solvent, such as diethyl ether.

Reread p.400-404, Ex. 3

Weak Acids

The best method of comparing the relative strengths of weak acids is to compare the relative values of their ionization constants, K_a.

Weak Acids: HA « H⁺ + A^-

Equations for ionization (produce H⁺ by equilibrium ionization)

Molecular weak acids

HF_(aq) « H⁺_(aq) + F^-_(aq)

Anions (rare)

HSO₄^-_(aq)^«H⁺_(aq)+ SO₄^2-_(aq)

Cations (all except Group 1, heavier Group 2 cations)

NH₄⁺_(aq)^«H⁺_(aq)+ NH_3(aq)

Zn(H₂O)₄²⁺_(aq)_«H⁺_(aq)+ Zn(H₂O)₃(OH)⁺_(aq)

Al(H₂O)₆³⁺_(aq) « H⁺_(aq)+ Al(H₂O)₅OH²⁺_(aq)

M(H₂O)_{4 or 6}^x+_(aq) « H⁺_(aq) + M(H₂O)_{3
or 5}OH^(x-1)+_(aq)

Ionization Constants of Aqueous Monoprotic Acids

Common Name            Formula          Constant        pKa

acetic acid            CH3COOH          1.75 x 10-5    4.756
ammonium ion           NH4+             5.60 x 10-10   9.252
anilinium ion          C6H5NH3+         2.54 x 10-5    4.596*
benzoic acid           C6H5COOH         6.31 x 10-5    4.200*
chloroacetic acid      CH2ClCOOH        1.36 x 10-3    2.866*
cyanic acid            HOCN             3.54 x 10-4    3.451
dichloroacetic acid    CHCl2COOH        5.68 x 10-2    1.246*
dimethylammonium ion   (H3C)2NH2+       1.82 x 10-11  10.739
ethanol                CH3CH2OH         1.31 x 10-14  13.882
formic acid            HCOOH            1.86 x 10-4    3.732
hydrazoic acid         HN3              2.37 x 10-5    4.625
hydrazinium ion        H2NNH3+          1.03 x 10-8    7.989
hydrochloric acid      HCl              greater than 1 negative
hydrocyanic acid       HCN              5.85 x 10-10   9.233
hydrofluoric acid      HF               6.94 x 10-4    3.159
hydroxylammonium ion   HONH3+           1.12 x 10-6    5.951*
hypochlorous acid      HClO             2.81 x 10-8    7.551
imidazolium ion        C3H3NNH2+        1.02 x 10-7    6.992*
lactic acid            H3CCHOHCOOH      1.37 x 10-4    3.863
methylammonium ion     H3CNH3+          2.39 x 10-11  10.622
ethanolammonium ion    HOCH2CH2NH3+     3.17 x 10-10   9.499*
nitric acid            HNO3            27.79          -1.444*
nitrous acid           HNO2             5.98 x 10-4    3.224
perchloric acid        HClO4           38.29          -1.583*
phenol                 C6H5OH           1.08 x 10-10   9.968*
pyridinium ion         C5H5NH+          6.80 x 10-6    5.167*
trimethylammonium ion  (H3C)3NH+        1.72 x 10-10   9.763
water                  H2O              1.01 x 10-14  13.994

Ionization Constants of Aqueous Polyprotic Acids

Common Name      Formula           Constant             pKa
arsenic acid     H3AsO4            K1 = 5.65 x 10-3    2.248
-                H2AsO4-           K2 = 1.75 x 10-7    6.757
-                HAsO42-           K3 = 2.54 x 10-12  11.596
boric acid       H3BO3             K1 = 5.78 x 10-10   9.238
carbonic acid    "H2CO3"           K1 = 4.35 x 10-7    6.361
-                HCO3-             K2 = 4.69 x 10-11  10.329
chromic acid     H2CrO4            K1 = 3.55          -0.550*
-                HCrO4-            K2 = 3.36 x 10-7    6.473*
citric acid      HOC(CH2COOH)3     K1 = 7.42 x 10-4    3.130*
-                -                 K2 = 1.75 x 10-5    4.757*
-                -                 K3 = 3.99 x 10-6    5.602*
EDTA             C2H4N2(CH2COOH)4  K1 = 9.81 x 10-3    2.008*
-                -                 K2 = 2.08 x 10-3    2.683*
-                -                 K3 = 7.98 x 10-7    6.098*
-                -                 K4 = 6.60 x 10-11  10.181*
glycinium ion    H3NCH2COOH+       K1 = 4.47 x 10-3    2.350*
-(glycine)       H2NCH2COOH        K2 = 1.67 x 10-10   9.778
hydrogen sulfide H2S               K1 = 1.02 x 10-7    6.992
-                HS-               K2 = 1.22 x 10-13  12.915
oxalic acid      HOOCCOOH          K1 = 5.40 x 10-2    1.268*
-                HOOCCOO-          K2 = 5.23 x 10-5    4.282
phthalic acid    C6H4(COOH)2       K1 = 1.13 x 10-3    2.946*
-                -                 K2 = 3.90 x 10-6    5.409*
phosphoric acid  H3PO4             K1 = 7.11 x 10-3    2.148
-                H2PO4-            K2 = 6.23 x 10-8    7.206
-                HPO42-            K3 = 4.55 x 10-13  12.342
succinic acid    C(CH2)2COOH       K1 = 6.21 x 10-5    4.207*
-                HOOC(CH2)2COO-    K2 = 2.31 x 10-6    5.636*
sulfuric acid    H2SO4             K1 > 1              negative
-                HSO4-             K2 = 1.01 x 10-2    1.994
sulfurous acid   H2SO3             K1 = 1.71 x 10-2    1.766
-                HSO3-             K2 = 5.98 x 10-8    7.223

Very Important** HA « H⁺ + A^-

K_a = [H⁺][A^-] pK_a = -logK_a_[HA]

Autoionization of Water

Water is very slightly ionized in to H⁺ and OH^- ions.

H₂O « H⁺+ OH^-2H₂O « H₃O⁺ + OH^-

Nature of the "H⁺" ion – preferably written as H₃O⁺ (hydronium ion)

Actual species is probably closer to H₉O₄⁺

Ion Product of Water, K_w K_w = [H⁺][OH^-] = 1.0´ 10^-14 at 25^oC KNOW THIS

Look up in your text Amphoteric and Amphiprotic. Use index.

pH and pOH

In 1909, a Danish biochemist, Soren Sorensen, defined a quantity called the "pH of a solution." It was defined as

pH = -log[H⁺]

What good is this? Why would we want to have such a definition?

Finding the pH of pure water:
Let x = mol/L of water that ionize. Then

(x)(x) = 1.0´ 10^-14 x² = 1.0´ 10^-14 x = [H⁺] = 1.0´ 10^-7 M

pH = -log 1.0´ 10^-7 M = -(-7) = 7

By a similar process, we can define the pOH of a solution, or pK_a of a weak acid, etc.

Relationship between pH and pOH

Since:

[H⁺] [OH^-] = 1.0´ 10^-14

log [H⁺] + log [OH^-] = log(1.0´ 10^-14) = -14

_{-log [H⁺] – log [OH^-] = 14

pH + pOH = 14}

What range can pH (and pOH) values assume?

On a blackboard----anything.

In reality, from about –1 to 15.

Neutral solution: pH = 7.0

Acidic solution: pH < 7.0

Basic solution: pH > 7.0

Suppose [H⁺] = 2.4´ 10^-6M; calculate pH

pH = -log₁₀ (2.4´ 10^-6) = 5.62

Suppose pH = 8.68; calculate [H⁺]

Use 10^x or "–" then INV and LOG keys;

[H⁺] = 10^-8.68 = 2.1´ 10^-9 M

pOH = -log₁₀[OH^-] ; pOH + pH = 14.00

What is [H₂O]?

Strong Acid

Practice Problem

Calculate the concentrations of H₃O⁺, HCl (molecules), OH^-, Cl^-, the pH, and the pOH of a 0.00800 M solution of HCl.

Note: On this and all subsequent problems, it will be assumed that the temperature is 25.0^oC unless stated otherwise.

Assumptions:

Since HCl is a strong acid (100% ionized), it is assumed that virtually all the H⁺in the solution comes from the HCl, and the amount coming form the water can be neglected.

HCl ® (100%) H⁺ + Cl^-

INT 0.00800 M 0 0

D -0.00800 M 0.00800 M 0.00800 M

EQU 0 0.00800 M 0.00800 M

PH = -Log [H⁺] = -Log 0.00800 = 2.097 NOTE sig Figs

POH = 14 – pH = 14.000 – 2.097 = 11.903

[OH^-] = 10^-pOH= 10^-11.903= 1.25´ 10^-12M

Strong Base

Practice Problem

Calculate the concentrations of Ba²⁺, OH^-, and the pH of a 0.0200 M solution of Ba(OH)₂.

Strong Base – How do you know?

Ba(OH)₂ ® (100%) Ba²⁺ + 2OH^-

INI 0.0200 M 0 0

D -0.0200 M 0.0200 M 0.0400 M

EQU 0 0.0200 M 0.0400 M

[OH^-] = 0.0400 M

[H⁺][OH^-] = 1.0´ 10^-14

[H⁺] = (1.0´ 10^-14/[OH^-]) = (1.0´ 10^-14/0.0400) = 2.5´ 10^-13M

pH = -Log [H⁺] = 12.60

Again NOTE the sig Figs

Variation of Kw With Temperature

Since the ionization of water is an equilibrium process, the extent of ionization, and thus the value of the equilibrium constant for the process, Kw, will vary with temperature.

The ionization of water is an endothermic process.

H₂O « H⁺ + OH^- DH = +55.9 kJ

According to Le Chatelier’s Principle, if temperature is increased, the system should shift to the right in an attempt to try and lower the temperature. This would result in higher concentrations of both H⁺ and OH^-, so K_w should increase with temperature.

Temperature ° C K_w

0 0.114´ 10^-14

10 0.292´ 10^-14

20 0.681´ 10^-14

25 1.01´ 10^-14

30 1.47´ 10^-14

40 2.92´ 10^-14

50 5.47´ 10^-14

60 9.61´ 10^-14

100 5.5´ 10^-13

Weak Acid

Practice Problem

Calculate the concentrations of H₃O⁺, OH^-, F^-, HF^-, the pH, pKa, and the % ionization of a 0.175 M solution of HF.

Ka for HF = 3.5´ 10^-4

HF « H⁺ + F^-

INI 0.175 M 0 0

D -x x x

EQU 0.175 - x x x

Ka = [H⁺][F^-]   =     (x)(x)     =     3.5´ 10^{-4


--------------
----------}              [HF]           0.175 - x

If we want to, we can solve this quadratic equation for ‘x’.
However, since HF is a weak acid (we know this because K_ais small), ‘x’ (the amount of HF ionized) must be a "small" number. If this is true, then 0.175-‘x’ would be approximately equal to 0.175, and we might be able to "neglect ‘x’". Let’s try this assumption and see what we obtain for an answer.

(x)(x) = 3.5´ 10^{-4

----------------}0.175 - x

x² = 6.125´ 10^-5

_{x = 7.83´ 10^-3 (2 sig figs
allowed)
But is this negligible?
It depends upon your standards.
Most textbooks suggest that you can "neglect ‘x’" if it is less
that 5% of the number it was subtracted from (or added to). The logic behind
this is that when we substitute molarities into an equilibrium constant
expression, we are only approximating the actual numbers, which should be
utilized anyway. We really should be using "activities," not
molarities, in the first place. If we accept this proposal, we now can see if
our assumption that ‘x’ was negligible was valid.
7.83´ 20^-3 ´
100 = 4.47%

-------------

0.175
Note: This is also the calculation of % ionization.
In this problem, we just made it!
Therefore:
[H⁺] = [H₃O⁺] = [F^-] = x = 7.8´
10^-3 M}

[OH^-] = 1.0´ 10^-14 = 1.0´ 10^-14 = 1.3´ 10^-12 M
------------- -------------
[H₃O⁺] 7.8´ 10^-3

[HF] = 0.175 - x = 0.175 – 0.0078 = 0.167 M

pH = -log(7.8´ 10^-3) = 2.11

pKa = -log Ka = 3.46

More Comment on the "Is ‘x’ Negligible?" Decision

What do you do if ‘x’ isn’t negligible?

Basically, you have two choices.

Solve the quadratic or any other equation that might be required.
Use the method of successive approximations. This involves neglecting ‘x’, solving the equation, then substituting this solution for ‘x’ back into the original equation and solving for the new, improved value for ‘x’. If this value differs significantly from the original solution for ‘x’, you substitute this new value into the original equation, solve again, etc., etc., etc. You keep doing this until you get two successive solutions for ‘x’ that are essentially the same.

Example of how this works—look at the last problem.

x₁ = 7.8262´ 10^-3

(x₂)(x₂) = 3.5´ 10^{-4

------------------------}0.175 - 0.0078262

x₂ = 0.0076492

(x₃)(x₃) = 3.5´ 10^{-4

---------------------------}0.175 - 0.0076492

x₃ = 0.0076533, Etc.

Practice Problem

The pH of a 0.345 M solution of a weak acid, HA, is 4.14. Calculate the ionization constant for this acid.

HA « H⁺ + A^-

INI 0.345 M 0 0

EQU

K_a = [H⁺][A^-]                  These are at equilibrium
        -----------
           [HA]

I know pH so I can get [H⁺] at equilibrium

pH = 4.14, Then [H⁺] = 10^-4.14 = 7.2´ 10^-5

So [A^-] = 7.2´ 10^-5 M

[HA] = 0.345 – 0.000072 » 0.345

K_a = (7.2´ 10^-5)² = 1.5´ 10^{-8

-------------------} 0.345

% Ionization = 7.2´ 10^-5 ´ 100%
------------
0.345

Polyprotic Acids

Two important things to remember are the ionization of polyprotic acids.

They only ionize one proton at a time.

Each successive ionization (usually) occurs to a much lesser extent than the previous ionization.

Stepwise ionization of H₂SO₄

H₂SO₄^®H⁺ + HSO₄^- K₁= very large

HSO₄^- « H⁺ + SO₄^2- K₂= 1.2´ 10^-2

Stepwise ionization of H₃PO₄

H₃PO₄ « H⁺ + H₂SO₄^-K₁= 7.52´ 10^-3

H₂PO₄^- « H⁺ + HPO₄^2-K₂= 6.23´ 10^-8

HPO₄^2- « H⁺ + PO₄^3- K₃= 2.2´ 10^-13

Weak Bases

Equation for ionization (produce OH^-ions by reaction with water molecule)

Molecular bases

NH_3(aq) + H₂O « NH₄⁺_(aq) + OH^-_(aq)

Anions derived from weak acids

F^-_(aq) + H₂O « HF_(aq) + OH^-_(aq)

B. Dissociation constant

Expression for K_b:

NH₃:                     K_b = [NH₄⁺] ´ [OH^-]
                                      ---------------------
                                              [NH₃]

Relation between K_b and K_a

K_b: B^- + H₂0 « HB + OH^-

K_a: HB « H⁺ + B^-

K_b ´ K_a = [HB] ´ [OH^-]   ´   [H⁺] ´ [B^-] = [H⁺] ´ [OH^-] = K_{w


-----------------------
--------------------}[B^-]                     [HB]

	K_a		K_b
HF	6.9 x 10^-4	F^-	1.4 x 10^-11
HC₂H₃O₂	1.8 x 10^-5	C₂H₃O₂^-	5.6 x 10^-10
NH₄⁺	5.6 x 10^-10	NH₃	1.8 x 10^-5

Strength of base is inversely related to that of conjugate weak acid.
See Page 5½ (My 8)

Calculation of [OH^-] in solution of weak base – Find pH of 0.10 M NaF solution?
100%

NaF ® Na⁺ + F^-

F- + H₂0 « HF + OH-

INI 0.10 M 0 0

D -x x x

EQU 0.10 – x x x

K_b = 1.4 ´ 10^-11 from above table

K_b = [HF] ´ [OH^-] = 1.4 ´ 10^-11 =    x²    =     x^{2


----------------------
--------       ---------}[F^-]                                0.10 – x     0.10

So x = 1.2 x 10^-6 M
and [H⁺] = 8.0 ´ 10^-9

Salts that Produce Acidic or Basic Solutions-Hydrolysis

Although we usually tend to think of salts as producing "neutral" solutions, many salts, when dissolved in water, actually produce a solution which is acidic or basic.

Examples:

NaCl ------------ neutral

KNO₃----------- neutral

NaC₂H₃O₂ ------ basic

KF --------------- basic

NaHSO₄ -------- acidic

NH₄Cl ---------- acidic

NaHCO₃ -------- basic

Na₂S ------------ basic

Al(NO₃)₃ ------- acidic

CaCl₂ ----------- neutral

KCl ------------- neutral

See p. 488 – 493

Lecture 3

Acid-Base Properties Salt Solutions

Must consider effect of cation and anion separately. Then combine these effects to give overall result for salt. P.493

Cations

Neutral- derived from strong bases:

Li⁺, Na⁺, K⁺, Ca²⁺, Sr²⁺, Ba²⁺

Acidic- all other cations, including those of the transition metals.

B. Anions

Neutral- derived from strong acids:

Cl^-, Br^-, I^-, NO₃^-, ClO₄^-, SO₄^2-

Acidic- HSO₄^-, H₂PO₄^-
Basic- all other anions. In general, an anion derived from a weak acid is expected to be basic.

C. Overall Results

Salt Cation Anion

NaNO₃ Na⁺ (N) NO₃^- (N) neutral

KF K⁺ (N) F^- (B) basic

FeCl₃ Fe³⁺ (A) Cl^- (N) acidic

See p. 493 Table 14.7- really know this.

What if both cation and anion hydrolyze (react with water). You can predict whether the solution is acid or base by comparing values of K_a and K_b.

Example:

Will a solution of Al₂(CO₃)₃ be acidic or basic?

The two reactions which can occur are:

Al(H₂O)₆³⁺ + H₂O « Al(H₂O)₅OH²⁺ + H₃O⁺

Or Al(H₂O)₆³⁺ « Al(H₂O)₅(OH^-)²⁺+ H⁺

And CO₃^2- + H₂O « HCO₃^- + OH^-

You need to look up the K_a of the acid and the K_b of the base. The large value wins!

The Formation of Salts from Acids and Bases

Neutral, Salt from a strong acid and a strong base:

NaCl Strong Acid HCl
Strong Base NaOH

Base, Salt from a weak acid and a strong base:

NaC₂H₃O₃ Weak Acid HC₂H₃O₃Strong Base NaOH

Acid, Salt from a strong acid and a weak base:

NH₄Cl Strong Acid HCl
Weak Base NH₄OH

?????? Salt of a weak acid and weak base

(NH₄)₂CO₃Weak Base CO₃^2-
Weak Acid NH₄⁺

Practice Problem

Calculate the pH of a 0.100 M solution of NaC₂H₃O₂.

Reaction involved is:

C₂H₃O₂^– + H₂O « HC₂H₂O₂ + OH^–

How to determine K_bC₂H₃O₃^– if it isn’t given.
The hydrolysis or "base" constant for the acetate ion is going to be related to the ionization constant, K_a, of its conjugate acid, namely acetic acid, HC₂H₃O₂.

The weaker the acid is (smaller K_a), the stronger the base must be (larger K_b).

K_a ´ K_b= K_w

The mathematical relationship between these two quantities is given by the equation:

K_b= K_w/K_a

Derivation of this relationship:

H₂O « H⁺ + OH^- K= K_w

C₂H₃O₂^- + H⁺ « HC₂H₃O₂ K= 1/K_a

C₂H₃O₂^- + H₂O « HC₂H₃O₂ + OH^- K_b = K_w/K_a

So K_b = 1.0´ 10^-14 = 5.68´ 10^{-10

-----------------}1.8´ 10^-14

Practice Problem—Actual Solution

Calculate the pH of a 0.100 M solution of NaC₂H₃O₂.

Always put an equation:

NaC₂H₃O₂ ® Na⁺ + C₂H₃O₂^– Goes 100%

C₂H₃O₂^– + H₂0 « HC₂H₃O₂^– + OH^– Does not go 100%

We want pH Need H⁺, get from OH^–

We can look up K_b or get from K_a

C₂H₃O₂^– + H₂0 « HC₂H₃O₂^– + OH-

INI 0.100 M Who cares 0 0

D -x | x x

EQU 0.100 – x ¯ x x

K_b = [HC₂H₃O₂] ´ [OH^-] = 5.68´ 10^-10    =       x^{2


----------------------------------
-------------}[C₂H₃O₂^-]                                          0.100 - x

Assume ‘x’ is small [put this on test] compared to 0.100

x² = 5.68´ 10^-11

_{x = [OH^-] = 7.54´ 10^-6

pOH = -log [OH^-] = -log 7.54´ 10^-6
= 5.123
pH = 14.00 – 5.123 = 8.877}

Bronsted-Lowry Definition of Acids and Bases

Is the second of the really important and popular definition of acids and bases.

Was proposed independently in 1923 by Tomas Martin Lowry in England and Johannes Nicolas Bronsted in Denmark. Bronsted really did the better work on the concept, so sometimes this is just referred to as the Bronsted definition.

Definition

Acid – a proton donor
Base – a proton acceptor

Differences from the Arrhenius Definition

In the Arrhenius definition, a substance is either an acid, a base, or neither. It never changes what it is. In the Bronsted-Lowry definition, a substance can be an acid one minute and a base the next. It depends upon what it is placed with.

Such substances are referred to as being amphiprotic.

Actually, virtually any substance containing protons could be amphiprotic under appropriate conditions. The term usually is used to refer to substances which can either donate or accept protons under "normal" conditions in aqueous solution such as HCO₃^- (but not HSO₄^-), H₂PO₄^-, HC₂O₄^-, HS^-, or even water itself.

When an Arrhenius acid reacts with an Arrhenius base, the products of the reaction are a salt and water.

When a B-L acid reacts with a B-L base, the products are another acid and another base, usually referred to as the conjugate acid and the conjugate base. The resulting solution (assuming the reaction takes place in solution) is not necessarily neutral. It can be anything. The only relevant question is to what extent does the reaction proceed.

You decide by considering the relative strengths of the two acid involved in the reaction (or the two bases). Essentially, a stronger acid and base are always converted into a weaker acid and base.

HF_(aq) + OH^-_(aq) « F^-_(aq) + H₂O

acid base

NH_3(aq) + H₂O « NH₄⁺_(aq) + OH^-_(aq)

base acid

HCl_(aq) + H₂O « H₃O⁺_(aq)+ Cl^-_(aq)

acid base

H₃O⁺ is referred to as the conjugate acid of H₂O

OH^- is the conjugate base of H₂O

Amphiprotic: Act as either an acid or a base: H₂O, HCO₃^-, H₂PO₄^- can donate or accept an H⁺.

Amphoteric: Can react with both H⁺ and OH^-. Al(OH)₃, Zn(OH)₂, Al.

Remember complex ion in the lab where both Acid and Base caused these to dissolve.

Lewis Definition of Acids and Bases (1923)

Acid – An electron pair acceptor (Electrophilic)

Base – An electron pair donor (Nucleophilic)

Examples of Lewis Acids:

BF₃, Al³⁺, Ag⁺, Zn²⁺, Cr³⁺, Ti⁴⁺, and many others.

Examples of Lewis Bases:

NH₃, H₂O, Co₃^2-, OH^-, F^-, and many others.

Lewis Acid-Base Reactions:

All Lewis acid-base reactions can be described as conjugation—two species simple bond together with what is referred to as a coordinate covalent bond.

"Classic" example:

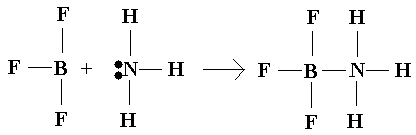BF₃ + NH₃ ® F₃BNH₃

H⁺_(aq) + H₂O ® H₃O⁺_(aq)

acid base

Back to the Class Notes Homepage

Maintained by: Chris Weilemann

Lee Marek

Salt	Cation	Anion
NaNO₃	Na⁺ (N)	NO₃^- (N)	neutral
KF	K⁺ (N)	F^- (B)	basic
FeCl₃	Fe³⁺ (A)	Cl^- (N)	acidic